We have already seen that if you pack people into a few locations, it tends to facilitate viral spread under our model.
But what if you are just packing people for a short amount of time into one location? Surely going for a soccer match or for a church sermon for an hour can’t be that bad?
That is, of course, wrong.
And you can see it clearly visually below in our tweaked model.
Let’s assume this parameters:
Same base model layout. 150 people live in this town, and there are 50 homes and 30 workplaces.
Schedules remain the same. People work from 9am to 5pm, else they are at home.
We are simulating the virus spread for 5 days.
However, on the 3rd day from 11am to 12pm, all the people in town gather for a church sermon. This is just to represent people clustering in one location for a short time - soccer match, Mardi Gras festival, etc.
I've disabled most parameters so you can concentrate on the visualization.
The one new parameter you can tweak is when the people in town go to the sermon - between days 0 and 4.
As expected, gathering lots of people in one or even a few locations is bad. It does not need to be for long, and just one hour in our model is enough.
Immediately what jumps out at you is that after the church sermon, the number of infected almost unfailingly spikes.
Especially once the town has a base of infected people, this multiplies exponentially, and then it quickly spreads to the rest of the town.
This is why mass gatherings (e.g. at a cinema, etc.) are not feasible in the short-term until the world can get a grip on COVID19 (antibody testing, vaccine, etc.)
I am going to take a short detour into probability on how the risk is compounded, and if you're not interested in the math, please feel free to skip!
As every sick person has a chance of infecting a healthy person at the same location (this is the infection chance variable), the more sick people there are in one location, the greater the risk is for the remaining healthy there.
Mathematically, the probability in this model is:
For any healthy individual, the chance of you getting sick by one sick person is the infection chance, or 2% (0.02). Thus the chance of you remaining healthy is
Because each chance of infection is independent, you can multiply them (
Let's say there are 3 sick people at your location. The chance of remaining healthy after factoring all 3 chances is then
Thus the compounded chance of getting sick for each healthy person at the location is
And just like in the baseline model, we're going to run 10,000 simulation runs, comparing a town without a church sermon and a town with one.
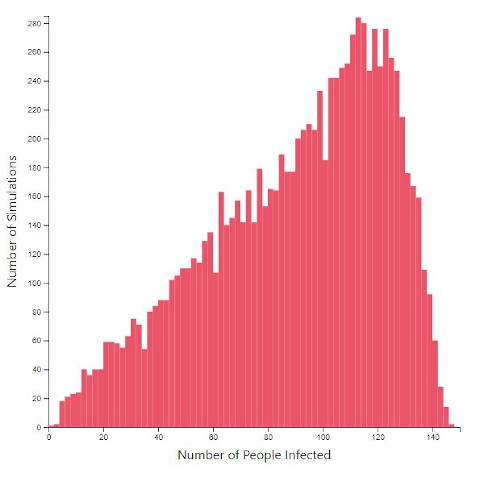
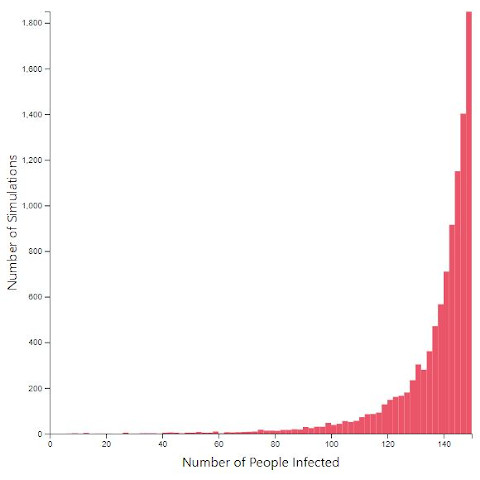
Parameters: 150 people town, 50 homes, 30 workplaces, 5 days simulation time, 2% infection rate.
Everything is the same except one town has a church sermon on day 3 at 11am where everyone attends. The other town everyone remains at work.
Both scenario simulations run 10,000 times.
As can be clearly seen, in the town with the church model, the infection rate is extremely likely to be high in this scenario.
Again, if you would like to see this and play with it yourself, check out the code on GitHub.